39组合总和
题目说明
给你一个 无重复元素 的整数数组candidates和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。对于给定的输入,保证和为 target 的不同组合数少于 150 个。
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
初观
以我不算多的算法经验来说,我第一直觉是动态规划算法,但是元素可以重用,脑子里就是这样一个思路。构建多维(不定维度)的参数矩阵,依次累加,但想到去重之类的逻辑还是感到相当棘手。
算法思路
回溯法
回溯法 采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:找到一个可能存在的正确的答案;在尝试了所有可能的分步方法后宣告该问题没有答案。
深度优先搜索
深度优先搜索 算法(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。这个算法会 尽可能深 的搜索树的分支。当结点 v 的所在边都己被探寻过,搜索将 回溯 到发现结点 v 的那条边的起始结点。这一过程一直进行到已发现从源结点可达的所有结点为止。如果还存在未被发现的结点,则选择其中一个作为源结点并重复以上过程,整个进程反复进行直到所有结点都被访问为止。
我刚开始学习「回溯算法」的时候觉得很抽象,一直不能理解为什么递归之后需要做和递归之前相同的逆向操作,在做了很多相关的问题以后,我发现其实「回溯算法」与「 深度优先遍历 」有着千丝万缕的联系。
算法的思路其实很简单,就是回溯与剪枝,使用递归实现。
- 回溯,用目标值逐步回溯(减去给定的数组元素),直到达到想要的结果(0)。
- 剪枝,递归实现的退出条件
- 达到目标(target = 0)
- 不可能再达到目标 (target < 0)
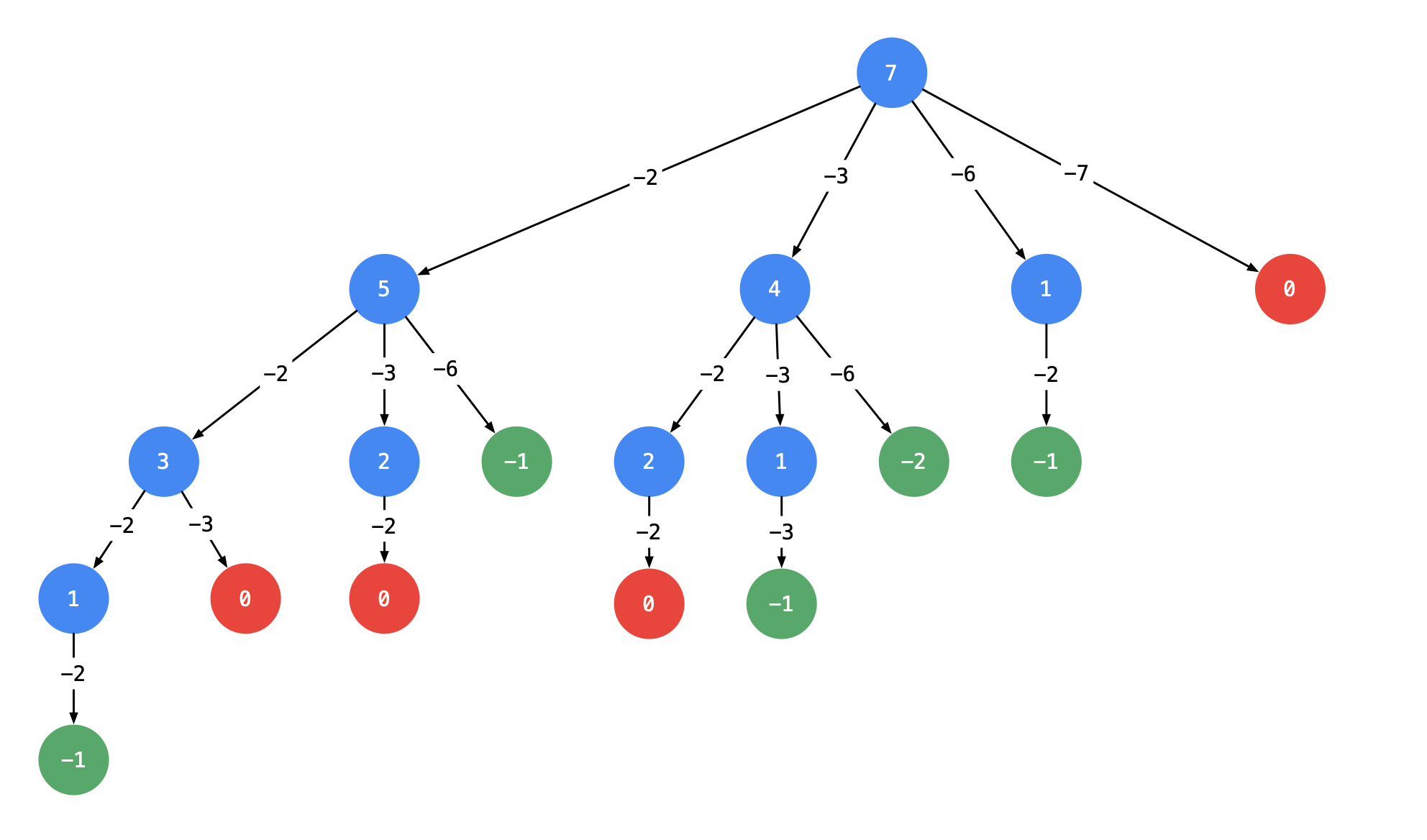
- 顺序,剪枝过程中如何去重,按顺序遍历以免出现[2,3,2]与[2,2,3]并存的情况
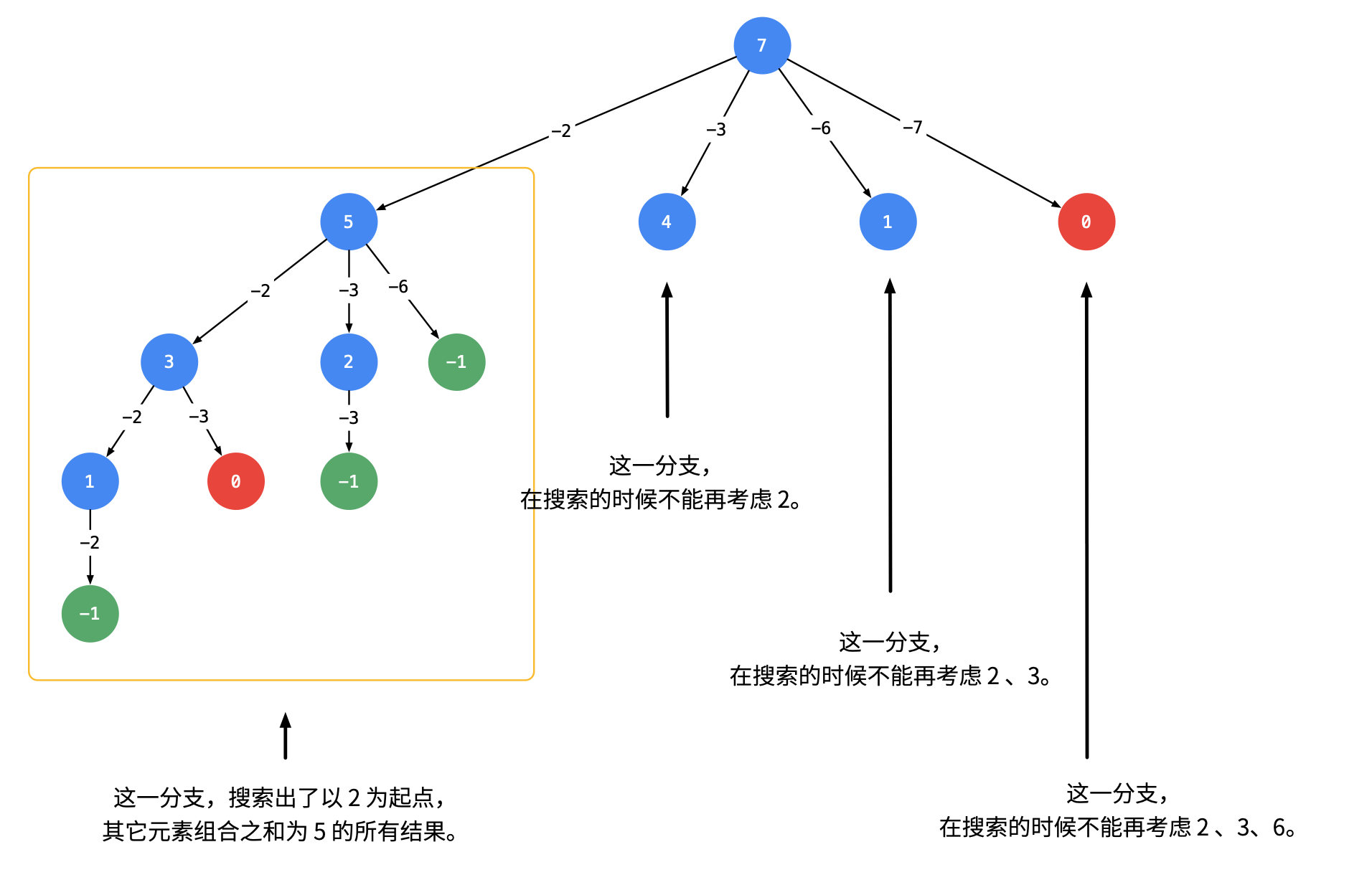
题解
理清思路和几个关键点后,实现就变得简单了。
class Solution {
public List<List<Integer>> combinationSum(int[] candidates, int target) {
//结果集
List<List<Integer>> results = new ArrayList<>();
//初始路径
LinkedList<Integer> path = new LinkedList<>();
conbineNext(candidates, target, 0, path, results);
return results;
}
/**
*
* @param candidates 数组
* @param target 本级目标
* @param startIndex 从哪个index开始遍历(去重)
* @param path 到目前位置遍历的路径
* @param results 结果集合
*/
private void conbineNext(int[] candidates, int target, int startIndex, LinkedList<Integer> path, List<List<Integer>> results){
if(target == 0){
results.add(new ArrayList<>(path));
}
if(target < 0){
return;
}
for(int i = startIndex; i< candidates.length;i++){
path.add(candidates[i]);
nextConbine(candidates, target - candidates[i], i, path, results);
//巧妙的状态重置,实际上在这里做了剪枝
path.removeLast();
}
}
}
46全排列
总体的思路是类似的
题目
给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。
输入:nums = [1,2,3] 输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
class Solution {
public List<List<Integer>> permute(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
boolean[] used = new boolean[nums.length];
permuteNext(nums, used, new LinkedList<>(), results);
return results;
}
private void permuteNext(int[] nums, boolean[] used, LinkedList<Integer> list, List<List<Integer>> results){
if(list.size() == nums.length){
results.add(new ArrayList<>(list));
return;
}
for(int i = 0; i<nums.length; i++){
if(used[i]){
continue;
}
used[i] = true;
list.add(nums[i]);
permuteNext(nums, used, list, results);
//这边非常巧妙,比起我原本的算法,减少了构造新列表的成本,总耗时减少了许多
used[i] = false;
list.removeLast();
}
}
}
47 全排列二
总体的思路是类似的,需要加入了不重复的判断,##提前剪枝##。
题目详情
给定一个##可包含重复数字##的序列 nums ,按任意顺序 返回所有不重复的全排列。
输入:
nums = [1,1,2]输出:[[1,1,2],[1,2,1],[2,1,1]]
解答
与46全排列相似,唯一不同的就是如何在遍历的时候排重。
- 原数组排序,将相同元素集中在一起
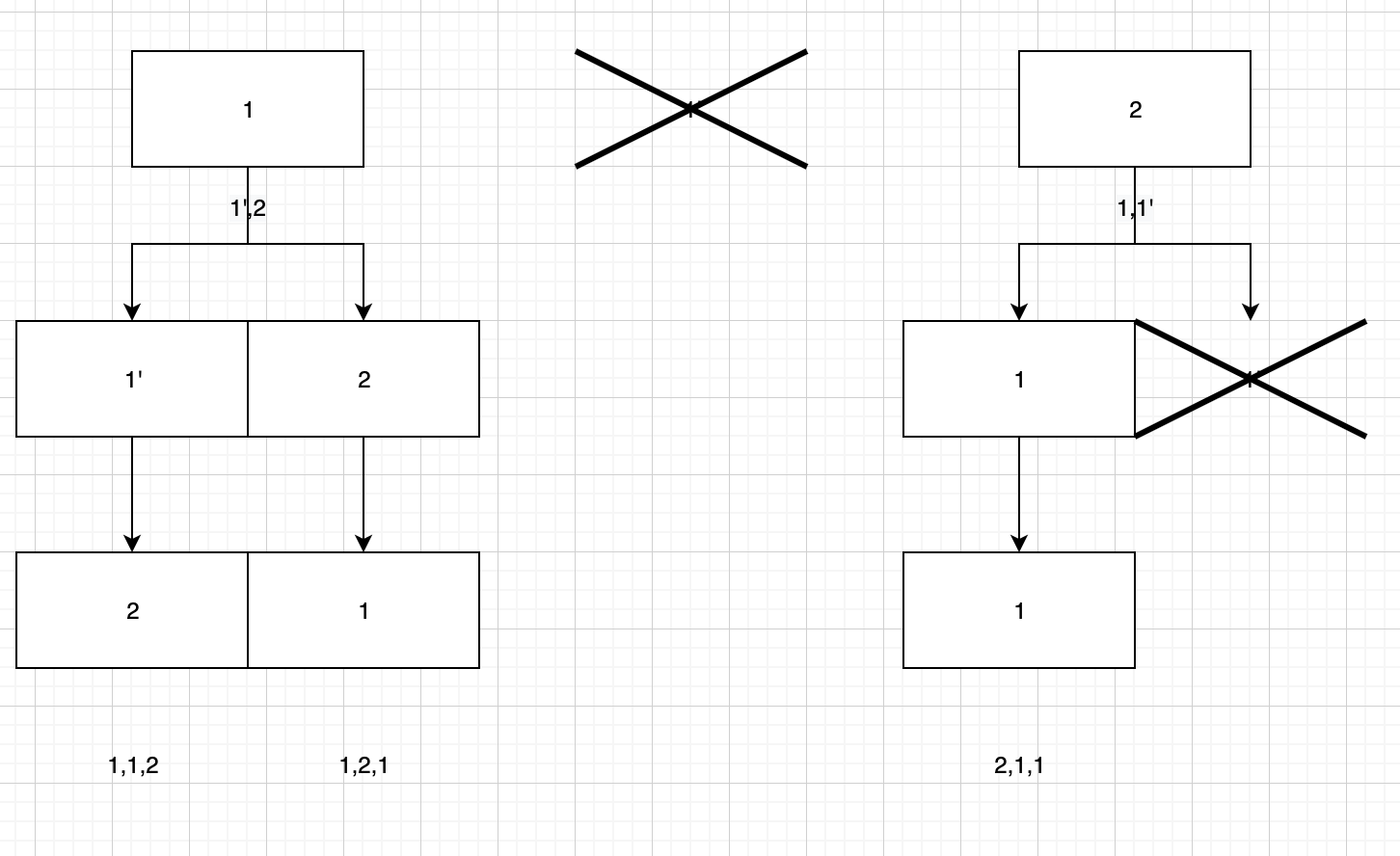
- 每层遍历时只使用相同元素中的第一个元素,比如顶层只遍历1,二层
2-[1,1']中遍历过1,则不遍历1‘。
class Solution {
public List<List<Integer>> permuteUnique(int[] nums) {
List<List<Integer>> results = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
boolean[] isUsed = new boolean[nums.length];
Arrays.sort(nums);
next(nums, isUsed, path, results);
return results;
}
private void next(int[] nums, boolean[] isUsed, LinkedList<Integer> path, List<List<Integer>> results){
if(path.size() == nums.length){
results.add(new ArrayList<>(path));
return;
}
for(int i=0;i<nums.length;i++){
//当前节点使用过返回
//或者不是排序数组中重复元素的第一个,比如[1,1,2],遍历第一层时不用index=1的1
if(isUsed[i] || (i>0 && nums[i] == nums[i-1] && !isUsed[i-1])){
continue;
}
isUsed[i] = true;
path.addLast(nums[i]);
next(nums, isUsed, path, results);
isUsed[i] = false;
path.removeLast();
}
}
}
78子集
题目详情
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
输入:
nums = [1,2,3]输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
解答
该题目一眼看来就是使用深度优先遍历或者回溯法来进行解答,按例子看如下图,发现规律
- 即如果使用了位置i的元素,那么后续只能从i+1的元素开始使用。
- 每一次的遍历都要把当前节点路径打印出来。

class Solution {
public List<List<Integer>> subsets(int[] nums) {
List<List<Integer>> result = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
//从0层开始,结果集加入空集
doSubsets(nums, 0, path, result);
return result;
}
/**
* curIndex,当层可以使用的元素下标起始点
* 可使用的元素即从curIndex到(nums.length - 1)
**/
private void doSubsets(int[] nums, int curIndex, LinkedList<Integer> path, List<List<Integer>> result) {
//记录本层路径
result.add(new ArrayList<>(path));
//处理当层从curIndex到(nums.length - 1)的元素
for (int i = curIndex; i <= nums.length - 1; i++) {
path.add(nums[i]);
//下一层
doSubsets(nums, i + 1, path, result);
//处理完成后回复状态进而处理本层下一个
path.removeLast();
}
}
}
79单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
输入:
board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]],word = "ABCCED"输出:true
题目解答
是个图深度优先遍历的问题,同时伴随着剪枝与退回,基本就是用回溯法解决。 注意点:
- 用过的不能再用,引入isUsed,且在路径探索失败时退回当前节点的使用
class Solution {
public boolean exist(char[][] board, String word) {
//两次循环,从二维数组中的每一个节点开始出发。
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (exist(board, i, j, word.toCharArray(), 0, new boolean[board.length][board[0].length])) {
return true;
}
}
}
return false;
}
public boolean exist(char[][] board, int i, int j, char[] word, int st, boolean[][] isUsed) {
//成功终止条件,此时证明word已经全部找到
if (st >= word.length) {
return true;
}
//越界的直接返回不存在
if (i >= board.length || j >= board[0].length || i < 0 || j < 0) {
return false;
}
//当前元素和下一个需要的字符不相等,直接返回不存在
if (board[i][j] != word[st]) {
return false;
}
//用过的不能再用,返回不存在
if (isUsed[i][j]) {
return false;
}
//当前节点可用,标记已使用
isUsed[i][j] = true;
//尝试寻找下一层
boolean exist = exist(board, i, j - 1, word, st + 1, isUsed) ||
exist(board, i, j + 1, word, st + 1, isUsed) ||
exist(board, i - 1, j, word, st + 1, isUsed) ||
exist(board, i + 1, j, word, st + 1, isUsed);
//如果不存在则当前路径失败,需要移除此时当前格子的占用
if(!exist){
isUsed[i][j] = false;
}
return exist;
}
}
494目标和
题目描述
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ’+’ 或 ‘-‘ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-‘ ,然后串联起来得到表达式 “+2-1” 。 返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
解答
第一思路暴力法,反正每个路径都试一下
class Solution {
private int sum = 0;
private int sumTarget;
public int findTargetSumWays(int[] nums, int target) {
sumTarget = target;
//下一个是+
doFind(nums, 0, 0, true);
//下一个是减
doFind(nums, 0, 0, false);
return sum;
}
public void doFind(int[] nums, int curSum, int curIndex, boolean isPlus) {
if (isPlus) {
curSum += nums[curIndex];
} else {
curSum -= nums[curIndex];
}
//如果当前是最后一个节点的就判断是否符合退出
if (curIndex + 1 == nums.length) {
if (curSum == sumTarget) {
sum++;
}
return;
}
//下一层的+或-
doFind(nums, curSum, curIndex + 1, true);
doFind(nums, curSum, curIndex + 1, false);
}
}
动态规划法(虽然这个并不属于这个回溯算法的文档,但反正也会有下期关于动态规划的文档)
求pos - nge = target pos - nge + pos + nge = target + pos + nge pos = (target + sum)/2 转化题目为求子集和为(target + sum)/2的组合数(这一步是最关键的)
dp[i][j]其中i为前i个元素中选出任意元素和为j的数量,因此求的为dp[nums.length - 1][pos]dp[i][j] = dp[i-1][j-nums[i - 1]] + 1 + dp[i-1][j] if(j -nums[i-1])其中dp[0][0] = 1,没有元素时只有和=0才是1;
-
递归实现
class Solution { /** * * @param nums * @param target * @return */ public int findTargetSumWays(int[] nums, int target) { int sum = Arrays.stream(nums).sum(); if (target > sum) { return 0; } int doublePosSum = sum + target; if (doublePosSum % 2 == 1) { return 0; } int posSum = doublePosSum / 2; return doFind(nums, nums.length, posSum); } private int doFind(int[] nums, int index, int posSum) { if (index == 0) { return posSum == 0 ? 1 : 0; } //不用这个元素 int noUseCurNum = doFind(nums, index - 1, posSum); if (posSum - nums[index - 1] >= 0) { return noUseCurNum + doFind(nums, index - 1, posSum - nums[index - 1]); } else { return noUseCurNum; } } } -
dp递归实现
class Solution { public int findTargetSumWays(int[] nums, int target) { int sum = Arrays.stream(nums).sum(); if (target > sum) { return 0; } int doublePosSum = sum + target; if (doublePosSum <0 || doublePosSum % 2 == 1) { return 0; } int posSum = doublePosSum / 2; int[][] dp = new int[nums.length + 1][posSum + 1]; dp[0][0] = 1; for (int i = 1; i <= nums.length; i++) { int num = nums[i - 1]; for (int j = 0; j <= posSum; j++) { if (j >= num) { dp[i][j] = dp[i - 1][j] + dp[i - 1][j - num]; } else { dp[i][j] = dp[i - 1][j]; } } } return dp[nums.length][posSum]; } } -
交替数组实现
class Solution { public int findTargetSumWays(int[] nums, int target) { int sum = Arrays.stream(nums).sum(); if (target > sum) { return 0; } int doublePosSum = sum + target; if (doublePosSum < 0 || doublePosSum % 2 == 1) { return 0; } int posSum = doublePosSum / 2; int[] dp = new int[posSum + 1]; dp[0] = 1; for (int i = 0; i <= nums.length - 1; i++) { int num = nums[i]; //逆序,保证本次dp[j]在遍历时,所有索引<j的都为上次的结果 for (int j = posSum; j >= num; j--) { dp[j] = dp[j] + dp[j - num]; } } return dp[posSum]; } }